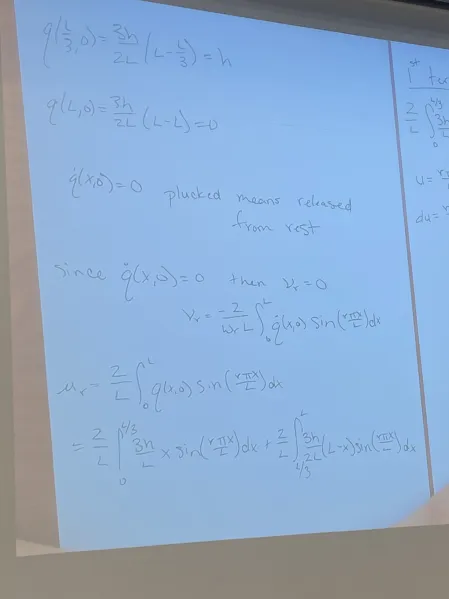2024-04-19 Loaded String

Announcements:

• HW 10 returned
• Do course evaluations

Continuous Systems

Loaded String Solutions

$$q_j=\sum _r{\beta }_r\sin \left(j\frac{r\pi }{n+1}\right)e^{i\omega t}$$

Where

$$\begin{array}{c}n=\text{number of masses}\\ r=\text{mode index}\end{array}$$

Frequencies given by:

$${\omega }_r=2\sqrt{\frac{\tau }{m\alpha }}\sin \left(\frac{r\pi }{2(n+1)}\right)$$ $$q_j(t)=\sum _r{\eta }_r(t)\sin \left(j\frac{r\pi }{n+1}i{\eta }_r\right)={\beta }_r{e}^{i\omega t}$$

Where ${\beta }_r={\mu }_r+i{\nu }_r$

$${\mu }_r=\frac{2}{n+1}\sum _j{q}_j(0)\sin \left(j\frac{r\pi }{n+1}\right)$$

Using initial position to solve for mu

$${\nu }_r=-\frac{2}{{\omega }_r(n+1)}\sum {\dot{q}}_j(0)\sin \left(j\frac{r\pi }{n+1}\right)$$

Using initial velocity to solve for nu

R goes up to number of masses. With 10 particles, there is 10 frequencies, and 10 sets of coefficients.

Using this discussion, we examine the consequence of allowing the number of particles on the string to be infinite, while maintaining a constant linear mass density.

As the number of string “particles” increases, the distance between them decreases

We need to make sure we don’t have infinite mass. Therefore

$$\rho =\frac{m}{d}=\text{constant}$$

Continuous String:

$$j\frac{r\pi }{n+1}\cdot \frac{d}{d}=r\pi \frac{x}{L}$$ $$jd=x$$

We need this to be a function of $x$ and $t$, as follows:

$$q(x,t)=\sum _r{\eta }_r(t)\sin \left(r\pi \frac{x}{L}\right)=\sum _r{\beta }_r{e}^{i{\omega }_{r}t}\sin \left(\frac{r\pi x}{L}\right)$$

There are infinite frequencies from infinite particles

Keeping only real terms (expanded ${\eta }_r$) and apply initial conditions

We get:

$$q(x,0)=\sum _r{\mu }_r\sin (\frac{r\pi x}{L})$$ $$\dot{q}(x,0)=-\sum _r{\omega }_r{\nu }_r\sin \left(\frac{r\pi x}{L}\right)$$

Multiply both sides by sin term, integrate from 0 → L. Using Kronecker delta, we get:

$$\frac{L}{2}{\delta }_{r,s}=\sin \frac{r\pi x}{L}\sin \frac{s\pi x}{L}$$ $${\mu }_r=\frac{2}{L}\underset{0}{\overset{L}{\int }}q(x,0)\sin \left(\frac{r\pi x}{L}\right)dx$$ $${\nu }_r=-\frac{2}{{\omega }_{r}L}\underset{0}{\overset{L}{\int }}\dot{q}(x,0)\sin \left(\frac{r\pi x}{L}\right)dx$$ $${\omega }_r=2\sqrt{\frac{\tau }{md}}\sin \left(\frac{r\pi }{2(n+1)}\right)$$ $$\frac{2}{d}\sqrt{\frac{\tau }{\rho }}\sin \left(\frac{r\pi d}{2L}\right)$$

As d goes to zero and particles go to infinity, we can use the small angle approx:

$$\frac{2}{d}\sqrt{\frac{\tau }{\rho }}\frac{r\pi d}{2L}$$ $${\omega }_r=\frac{r\pi }{L}\sqrt{\frac{\tau }{\rho }}$$

Tension over density, the second term, is the velocity of the wave on the string.

Plucked String:

at $\frac{L}{3}$

figure here

String, plucked to height h at l/3

In the space $x<\frac{L}{3}$

Slope

$$\frac{\Delta y}{\Delta x}=\frac{3h}{L}$$ $$y=ax+b=\frac{3h}{L}x+b$$ $$q(x,0)=\frac{3h}{L}x;0\le x\le \frac{L}{3}$$ $$0=\frac{3h}{L}(0)+b⟹b=0$$

In the space $\frac{x>L}{3}$ Slope given by:

$$-\frac{3h}{2L}$$ $$y=-\frac{3h}{2L}x+b$$ $$0=-\frac{3h}{2L}(L)+b⟹b=\frac{3h}{2}$$ $$\begin{gathered} q(x,0)=\frac{3h}{2L}(L-x); \\ \frac{L}{3}\le x\le L \end{gathered}$$