2024-01-03 Classical Review

Classical mechanics

• Used in 1687 to 1905, 1905 was Einstein’s “miracle” year
• Classical mechanics works well for low speed, not high gravity areas.
• Newtonian Mechanics
  • Based on the concept of forces $\vec{F}$
  • Think about incline plane problems, free body diagrams, Dr Korniss
  • 
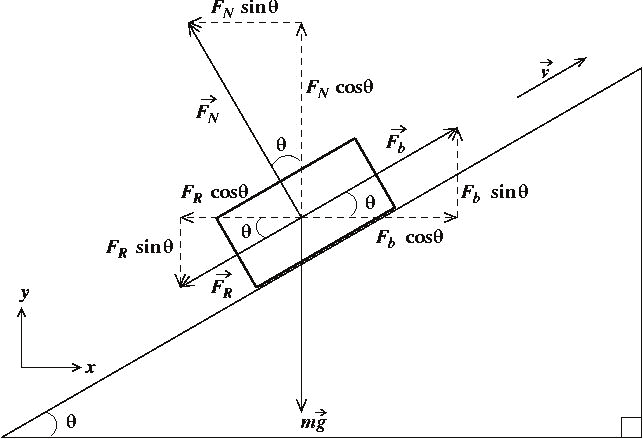
  • Dot notation for derivatives, $\dot{x}$ is first time derivative, $\ddot{x}$ is second time derivative.
• Lagrange/Hamiltonian mechanics
  • Based on energy (kinetic and potential)
  • By understanding the energy of a system, we can understand the system.
  • This is very powerful, especially in complex systems
  • Does not replace Newtonian mechanics. Sometimes Newtonian mechanics is faster.
  • What kinds of problems are better?
    • Linear motion (ez)
    • Rotational motion (chemistry (molecules), aero. mechanics (spacecraft and satellites))
    • Oscillatory motion / vibrations (phonons/molecular vibrations)
      • Acoustics
      • Waves

Newtonian Review

Newtons Laws of motion

1. An object in motion, stays in motion and an object at rest stays at rest, unless acted on by outside forces. This is known as inertia. $\vec{\Sigma }=0\to \vec{v}=0$
2. Acceleration imparted by a force to an object is the magnitude of the force divided by the object mass. $\Sigma \vec{F}=m\vec{a}$
3. Every action invokes an equal and opposite reaction. $|{\vec{F}}_{12}|=|{\vec{F}}_{21}|$ This is the most misunderstood of the third laws. Needs to be a “target-source” pair

Classical motion, acceleration and energy

• Acceleration is equal to second position derivative with respect to time.

$$\vec{a}=\frac{d\vec{v}}{dt}=\frac{d^2\vec{x}}{d{t}^2}$$ $$\vec{a}=\ddot{\vec{x}}=\vec{v}$$

• Momentum is : $\vec{p}=m\vec{v}$

$$\vec{\Sigma }\vec{F}=\frac{d\vec{p}}{dt}=m\frac{d\vec{v}}{dt}$$

• Mechanical energy: $E=T+U$ ($T$ is kinetic energy, not K)

$$T=\frac{1}{2}m{v}^2$$

• Angular momentum: $\vec{L}=\vec{r}\times \vec{p}=I\vec{\omega }$
  • They lied about moment of inertia smh dr korniss
• Mechanical energy is conserved if all forces acting on the object are conservative forces.
  • A force is a conservative force if $\oint \vec{F}\cdot d\vec{r}=0$
  • Path does not matter.
  • $\int \vec{F}\cdot d\vec{r}$ is equal to work
  • Think about Dr. Martin waving his phone around. As long as it goes back to where it starts its going to be a conservative force (for gravity)

Work Energy Theorem

$$T_F-T_I=W$$

• Application of newtons laws to mechanical problem solving.
  1. Identify all forces $\vec{F}$
  2. Describe magnitude and direction of all forces
     • Think free body diagram
  3. Write down Newtons second law
     • ${\vec{F}}_{net}=m\vec{a}=\frac{d\vec{v}}{dt}$
  4. Solve the differential equation
     • ${\vec{F}}_{net}=m\frac{d^{2}x}{d{t}^2}$
     • Generally, we must solve a second order differential equation of form

$$m\frac{d^{2}x}{d{t}^2}=\vec{F}(\vec{x},\vec{x},t)$$

Special cases

• Constant force. Independent of position, velocity and time. $\vec{F}=c$
  • Forces with constant acceleration.
    • Free fall acceleration, $\vec{F}=mg$
    • Static and dynamic friction
• Force Dependent on position only $\vec{F}=\vec{F}(\vec{x})$
  • Electromagnetism, gravity, and spring
    • Harmonic oscillator
      • $\vec{F}=-k\vec{x}$
    • Coulombic Forces
      • $\vec{F}=\frac{k{q}_1{q}_2}{r^2}\vec{r}$
    • Gravitational forces
      • $\vec{F}=\frac{G{m}_1{m}_2}{r^2}\vec{r}$
• Force dependent on velocity $\vec{F}=\vec{F}(\vec{\dot{x}})$
  • Air and water resistance (drag forces)
    • $\vec{F}=\pm k{\vec{x}}^n$
  • Magnetic forces
• More complex systems $\vec{F}=\vec{F}(\vec{\dot{x}},\vec{x},t)$
  • Damped oscillator driven by an external time-dependent force

Constant Force Example

• For a case with a constant force $\vec{F}=c$
  • If the force is constant the acceleration is also constant

$$\vec{F}=m\vec{a}=c$$ $$m\frac{dv}{dt}=ma$$ $$\frac{dv}{dt}=a$$ $$dv=adt⟹\int dv=\int adt=a\int dt$$ $$v=at+c_1$$

• Then you can find position

$$v=\frac{dx}{dt}=at+c_1$$ $$dx=atdt+c_{1}dt$$

• Integrate both sides

$$\int dx=a\int tdt+c_1\int dt$$ $$x=\frac{1}{2}a{t}^2+c_{1}t+c_2$$

$c_1$ and $c_2$ come from initial conditions

• The initial conditions are what makes the problems unique

$$x(t=0)=x_0\&v(t=0)=v_0$$ $$x(t=0)=c_2=x_0$$

see problem 3 on hw?

$$v(t=0)=c_1=v_0$$ $$x(t)=\frac{1}{2}a{t}^2+v_{0}t+x_0$$

This is the equation of motion ^

$$v(t)=at+v_0$$

Classical mechanics is deterministic. You need to know all the needed forces to solve it. This is hard.

Time dependent force $F(t)$

$$m\ddot{x}=F(t)$$ $$m\frac{d^{2}x}{d{t}^2}=F(t)=m\frac{dv}{dt}$$

Use separation of variables with velocity and time

$$dv=\frac{1}{m}F(t)dt$$ $$\int dv=\frac{1}{m}\int F(t)dt$$ $$v=\frac{1}{m}\int F(t)dt+c_1$$

Now find position

$$v=\frac{1}{m}\int F(t)dt+c_1=\frac{dx}{dt}$$ $$\int dx=c_1\int dt+\frac{1}{m}\int \left[\int F(t)dt\right]dt$$ $$x=c_2+c_{1}t+\frac{1}{m}\int \left[\int F(t)dt\right]dt$$

With a time dependent force you can solve this out.

Velocity Dependent Force $\vec{F}(\vec{v}=\vec{F}(\vec{\dot{x}}))$

• See problem 3!!! Make sure to put both forces as F(v)

$$F(v)=m\frac{dv}{dt}$$

Separation of variables

$$dt=m\frac{dv}{F(v)}$$ $$\int dt=m\int \frac{dv}{F(v)}$$

Rearrange $t(v)$ to $v(t)$

$$v(t)=\frac{dx}{dt}$$ $$x(t)=\int v(t)dt$$

Alternatively:

$$F(v)=m\frac{dv}{dt}=m\frac{dv}{dx}\frac{dx}{dt}$$ $$\frac{dv}{dt}=v$$ $$=mv\frac{dv}{dx}$$

use this 4a

$$\int dx=\int mv\frac{dv}{F(v)}$$ $$x(v)\to v(x)$$ $$v=\frac{dx}{dt}$$ $$\int dt=\int \frac{dx}{v(x)}$$

Use this for HW#4!!

Position dependent force

These forces are conservative forces

$$F(x)=m\frac{dv}{dt}$$

This is not integrable. (no seperation of variables)

Use chain rule!

$$F(x)=m\frac{dv}{dt}\frac{dx}{dx}$$ $$F(x)=m\frac{dv}{dt}\frac{dx}{dx}=m\frac{dv}{dx}\frac{dx}{dt}=mv\frac{dv}{dx}$$ $$\int F(x)dx=\int mvdv$$

Lets look at $F(x)=mv\frac{dv}{dx}$

Right side can be transmogrified into $\frac{1}{2}m{v}^2$ by taking the LHS to be $F(x)=\frac{dT}{dx}$ Taking the position derivative of kinetic energy yields $mv\frac{dv}{dx}$ and force

$${\int }_{x_0}^{x}F(x^{\prime })d{x}^{\prime }={\int }_{T_0}^{T}dT$$

This yields:

$$T-T_0={\int }_{x_0}^{x}F(x^{\prime })d{x}^{\prime }$$

Which is the work-kinetic energy system

$$w=\Delta T$$

This is time independent

We are introducing a function $U(x)$ such that

$$F(x)=-\frac{dU(x)}{dx}$$

The name of this thing is potential energy

$$\int dU(x)=-\int F(x)dx$$ $$U(x)=-{\int }_{x_0}^{x}F(x)dx$$

We can define an $x_0$ arbitrarily, as well as positive, negative etc. Make sure you keep your systems consistent.

$${\int }_{x_0}^{x}F(x)dx=T-T_0={\int }_{x_0}^x\left[-\frac{dU(x)}{dx}\right]dx$$ $$=-{\int }_{x_0}^{x}dU(x)=-U(x){|}_{x_0}^x$$ $$=-U(x)+U(x_0)$$ $$T-T_0=T(x)-T(x_0)=-U(x)+U(x_0)$$ $$T(x)+u(x)=T(x_0)+U(x_0)=\mathbf{E}$$

This $\mathbf{E}$ is the total mechanical energy. It is Conserved, as per the conservation of mechanical energy. All this came from the force that was based on position. Pretty neat.

Conservation of mechanical energy

$$\Delta T=-\Delta U$$

for position-dependent (conservative) forces

Can solve mechanical systems using energy conservation to get equation of motion

$$E=T+U=\frac{1}{2}m{v}^2+U(x)$$ $$=\frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+U(x)$$

Solve for $\frac{dx}{dt}$

$$\frac{dx}{dt}=\pm \sqrt{\frac{2}{m}(E-U(x))}$$ $$\int dt=\int \pm [\frac{2}{m}(E-U(x)){]}^{-1/2}dx$$ $$t(x)=t_0+{\int }_{x_0}^x\frac{dx}{\pm \sqrt{\frac{2}{m}(E-U(x))}}$$

There will be 2 solutions. Only 1 will actually describe your system. (Have physical meaning). Must meet the condition that

$$E-u(x)\ge 0$$

Motion is limited to energies where $E>u(x)$

We can analyze motion of a system by creating a plot of $u(x)$ vs $x$

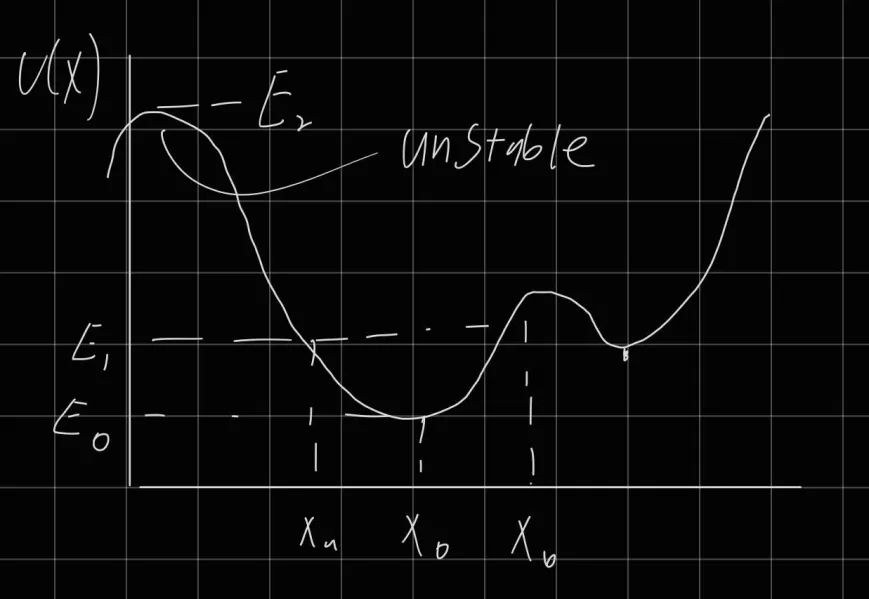
• $x_0$ is the stable equilibrium point
• equilibrium $=\frac{du}{dx}=0$
• $\frac{d^{2}U}{d{x}^2}$ to determine stable/unstable
• If second derivative is positive it is stable it is also a smiley face
• If second derivative is negative it is unstable it is also a frowny face

$$x_a<x<x_b$$

bounded motion (oscillatory behavior)

For what cases is it possible to to solve equation of motion using separation of variables?

Ex 1.)

$$F(x,t)=F(x)g(t)=m\frac{dv}{dt}$$

Use chain rule

$$=m\frac{dv}{dx}\frac{dx}{dt}=m\frac{dv}{dx}v$$

This is not integrable via separation

Ex 2.)

$$F(v,t)=F(v)g(t)=m\frac{dv}{dt}$$ $$g(t)dt=\frac{mdv}{F(v)}$$

integrate both sides

$$\int g(t)dt=\int \frac{m}{F(v)}dv$$

Example

$$F(v,t)=vt$$ $$vt=m\frac{dv}{dt}⟹\int tdt=\int \frac{m}{v}dv$$ $$\frac{t^2}{2m}=m\ln (v)$$ $$v=e$$

Example 2

$$F(x,v)=F(x)g(t)=m\frac{dv}{dt}$$

Chain rule:

$$=m\frac{dv}{dx}\frac{dx}{dt}=mv\frac{dv}{dx}$$ $$F(x)dx=\frac{mdv}{g(v)}$$