2024-02-09 Angular and Hamiltonian

Exam Logistics

• Tuesday 2/13 form 8-9:50
• 4 problems, each problem should be ~ half hour
• Concepts covered
  • 2024-01-03 Classical Review
  • 2024-01-19 Special Relativity
    • Have numbers in it, will be simple numbers
    • Boost Equations
    • Length contraction/time dilation equations
    • Velocity transformations
  • 2024-01-23 Lagrangian Mechanics
    • Not doing forces of constraint
  • 2 problems on Lagrangian Mechanics, 1 on classical review, one on special relativity.
  • No calculators, no crib sheet
  • Any non-standard integral will be given
  • Use problems in the book for review

Conservation of Angular Momentum

Continued from 2024-02-06 Hamilton and Conservation

• Lagrangian is invariant under rotation
• For some vector $\vec{r}$

$$L(\vec{r}+\delta \vec{r})=L(\vec{r})$$ $$\delta \vec{r}=\delta \vec{\theta }\times \vec{r}$$

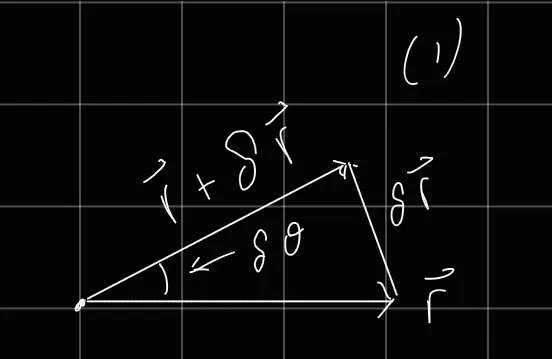
Then

$$\delta \dot{\vec{r}}=\delta \vec{\theta }\times \dot{\vec{r}}$$ $$L(\vec{r}+\delta \vec{r})-L(\vec{r})=\delta L$$ $$\delta L=\sum _i\frac{\partial L}{\partial x_i}\delta x_i+\sum _i\frac{\partial L}{\partial {\dot{x}}_i}\delta {\dot{x}}_i\text{\hspace{1em}(0)}$$ $$\frac{dL}{d{\dot{x}}_i}=P_i\text{\hspace{1em}(1)}$$ $$\frac{dL}{d{x}_i}={\dot{P}}_i\text{\hspace{1em}(2)}$$

Plug eqs 1 and 2 into 0

$$\delta L=\sum _i{\dot{P}}_i\delta x_i+P_i\delta {\dot{x}}_i$$

We can use the dot product to simplify this into the following:

$$\delta L=\dot{\vec{P}}\cdot \delta \vec{r}+\vec{P}\cdot \delta \dot{\vec{r}}$$

Simplify with chain rule

$$=\vec{\dot{P}}\cdot (\delta \vec{\theta }\times \vec{r})+\vec{P}\cdot (\delta \vec{\theta }\times \dot{\vec{r}})$$ $$=\delta \vec{\theta }\cdot (\vec{r}\times \vec{\dot{P}})+\delta \vec{\theta }\cdot (\dot{\vec{r}}\times \vec{P})$$ $$\delta L=\delta \vec{\theta }\frac{d}{dt}(\vec{r}\times \vec{P})$$

Angular Momentum formulas

Angular momentum is conserved if L is invariant under rotation. If a system is symmetric about an axis, then angular momentum in that direction (of axis ) is conserved.

Examples with uniform circular motion

in x-y plane

• Symmetry about z-axis, so $L_z$ is conserved Cylindrical symmetry $L_z$ conserved. Spherical symmetry $\vec{L}=$ constant

goddamn

Hamilton Dynamics

Canonical (inherent) equations of motion. For example, the canonical equation of motion for Lagrangian mechanics is the Euler-Lagrange Equation

Aside: Hamiltonian mechanics and dynamics are very useful for things that are not classical. They are, however, very useful for quantum physics. It produces first order differential equations, which was very useful hundreds of years ago when computers didn’t exist.

Transforming the Lagrangian into the Hamiltonian The Lagrangian is a function of position, velocity and time

$$L(q,\dot{q},t)\to H(q,p,t)$$ $$H=\sum _j{\dot{q}}_j\frac{\partial L}{\partial {\dot{q}}_j}-L$$ $$=\sum _j{P}_j{\dot{q}}_j-L(q_k,{\dot{q}}_k,t)$$ $${\dot{q}}_j={\dot{q}}_J(q_k,p_k,t)$$ $$dH=\sum _k\left[\frac{\partial H}{\partial q_k}d{q}_k+\frac{\partial H}{\partial P_k}d{p}_k\right]+\frac{\partial H}{\partial t}dt$$ $$\frac{\partial H}{\partial q_k}=P_k\frac{\partial {\dot{q}}_k}{\partial q_k}-\frac{\partial L}{\partial q_k}-\frac{\partial L}{\partial {\dot{q}}_k}\frac{\partial {\dot{q}}_k}{\partial q_k}$$ $$\frac{\partial H}{\partial q_k}=-\frac{\partial L}{\partial q_k}=-{\dot{p}}_k$$ $$\frac{\partial H}{\partial p_k}={\dot{q}}_k+P_k\frac{\partial {\dot{q}}_k}{\partial p_k}-\frac{\partial L}{\partial {\dot{q}}_k}\frac{\partial {\dot{q}}_k}{\partial p_k}={\dot{q}}_k$$ $$dH=\sum _k[-{\dot{p}}_{k}d{q}_k+{\dot{q}}_{k}d{p}_k]-\frac{\partial L}{\partial t}dt$$

Hamiltonian equations of motion:

$$\frac{\partial H}{\partial q_k}=-{\dot{P}}_k$$ $$\frac{\partial H}{\partial P_k}={\dot{q}}_k$$ $$\frac{\partial H}{\partial t}=-\frac{\partial L}{\partial t}$$

if

$$\frac{dH}{d{q}_k}=0\therefore P_k\text{ = constant}$$

if

$$\frac{dH}{d{P}_k}=0\therefore q_k\text{=constan}$$

Example: Free particle of mass m in 1 dimension

$$x=q$$ $$L=T>q?>0=\frac{1}{2}m{\dot{q}}^2$$

Need generalized momentum. Ignore weird part above, i couldnt really read his handwriting.

$$H=\dot{q}\frac{\partial L}{\partial \dot{q}}-L$$ $$\frac{\partial L}{\partial \dot{q}}=m\dot{q}=P$$ $$\dot{q}=\frac{P}{m}$$ $$=\dot{q}\cdot m\dot{q}-\frac{1}{2}m{\dot{q}}^2=\frac{1}{2}m{\dot{q}}^2$$

This is not correct! no velocity allowed

$$H=H(q,p,t)$$ $$H=\frac{1}{2}\frac{P^2}{m}$$ $$\frac{\partial H}{\partial p}=\frac{p}{m}$$ $$\frac{\partial H}{\partial p}=\frac{p}{m}=\dot{q}$$ $$\frac{\partial H}{\partial q}=0=-\dot{p}$$ $$\frac{dp}{dt}=0\text{ and }p=\text{ constant}$$ $$\frac{dq}{dt}=\frac{p}{m}$$ $$\int dq=\int \frac{p}{m}dt$$ $$q=\frac{p}{m}t+c_1$$

Which is equiv. to

$$x=v_{0}t+x_0$$

Example Harmonic oscillator

$$L=\frac{1}{2}m{\dot{x}}^2-\frac{1}{2}k{x}^2$$ $${\omega }^2=\frac{k}{m};k=m{\omega }^2$$ $$\frac{\partial L}{\partial \dot{x}}=m\dot{x}=P_x⟹\dot{x}=\frac{P_x}{m}$$ $$H=\dot{x}\frac{\partial L}{\partial \dot{x}}-L=m{\dot{x}}^2-\left(\frac{1}{2}m{\dot{x}}^2-\frac{1}{2}k{x}^2\right)$$ $$=\frac{1}{2}m{\dot{x}}^2+\frac{1}{2}k{x}^2$$

This is not the Hamiltonian! Has velocity, not momentum

$$=\frac{1}{2}\frac{P_x^2}{m}+\frac{1}{2}k{x}^2$$ $$\frac{dH}{dx}=kx=-{\dot{P}}_x$$ $$\frac{dH}{d{P}_x}=\frac{P_x}{m}=\dot{x}$$ $$-\dot{P}=kx=m{\omega }^{2}x$$ $$P=m\dot{x}=m\dot{x}$$ $$\frac{i}{m\omega }\cdot (-\dot{P})=m{\omega }^{2}x\cdot \frac{i}{m\omega }$$ $$-\frac{i\dot{P}}{m\omega }=i\omega x$$ $$-\frac{i\dot{P}}{m\omega }+\frac{P}{m}=i\omega x+\dot{x}$$ $$\dot{x}+\frac{i\dot{p}}{m\omega }=\frac{p}{m}-i\omega x=-i\omega \left(x+\frac{ip}{m\omega }\right)$$ $$z=x+\frac{ip}{m\omega }$$ $$\dot{z}=\dot{x}+\frac{i\dot{p}}{m\omega }$$ $$\dot{z}=-i\omega z$$ $$z=z_0{e}^{-i\omega t}$$

Alternative:

$$H=\frac{p^2}{2m}+\frac{k}{2}{x}^2$$

Choose coordinates such that H is cyclic

$$\left(\frac{dH}{d{q}_0}\right)=0$$ $$P_{1}x\to P_{1}Q$$ $$P=\sqrt{2m\omega P}\cos Q$$ $$x=\frac{\sqrt{2m\omega P}}{m\omega }\sin Q$$

What the fuck is this.

$$H=\frac{1}{2m}2m\omega P{\cos }^{2}Q+\frac{m{\omega }^2}{2}\frac{2m\omega P}{m^2{\omega }^2}$$ $$H=\omega P$$ $$\frac{\partial H}{\partial Q}=0=-\dot{P}$$ $$P=\text{constant}=\frac{H}{\omega }=\frac{E}{\omega }$$ $$\frac{\partial H}{\partial P}=\omega =\dot{Q}$$ \dot{Q} = \omega t + \phi $$Go back?

p=\sqrt{ 2mE } \cos(\omega t+\phi)

x = \sqrt{ \frac{2E}{m\omega^{2}} } \sin(\omega t+\phi)

### Conservation Laws - For a given variable, q, p or t, to see if that quantity is conserved we should check the total time derivative. - $F(q,p,t)$ general function of $q_{i},P_{i}$ and $t$

\frac{ d F }{ d t } = \frac{ d F }{ d t } + \sum_{i} \left( \frac{ d F }{ d q_{i} } \dot{q}{i} + \frac{ d F }{ d P{i} }\dot{P}_{i} \right)

\frac{dF}{dt} = \frac{ d F }{ d t } + \sum_{i}\left[ \frac{ \partial F }{ \partial q_{i} } \frac{ \partial H }{ \partial P_{i} }-\frac{ \partial F }{ \partial P_{i} }\frac{ \partial H }{ \partial q_{i} } \right]

$$Thebracketcanbeexpressedcompactlyasa[[Poissonbracket]]$$

\left[ \frac{ \partial F }{ \partial q_{i} } \frac{ \partial H }{ \partial P_{i} }-\frac{ \partial F }{ \partial P_{i} }\frac{ \partial H }{ \partial q_{i} } \right] \equiv {H,F}

F is conserved if $\frac{dF}{dt}=0$ Implies $\frac{ d F }{ d t }=0 \to \{H,F\}=0$ This is especially useful when we transition from classical to quantum mechanics. For a problem 1. Determine the classical Hamiltonian 2. Transition by replacing q and p by their operators

{H,q}=[\hat{H}\hat{Q}-\hat{Q}\hat{H}]

q \to \hat{Q}

p \to \hat{P}

p_{x} = i\hbar \frac{d}{dx}

$$Nexttopicis[[CentralForces]]$$