2024-01-26 Calc. of Variations

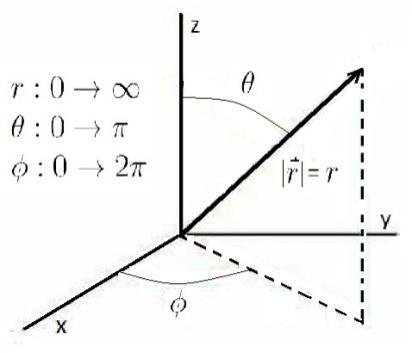
Spherical Coordinates and the Lagrangian

$$x=r\cos \varphi \sin \theta$$ $$y=r\sin \varphi \sin \theta$$ $$z=r\cos \theta$$

Energy:

$$T=\frac{1}{2}m({\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2)$$ $$\frac{d}{dt}\frac{\partial L}{\partial \dot{q}i}-\frac{\partial L}{\partial qi}=0$$

NB: what depends on time? all 3!

$$\dot{z}=\frac{d}{dt}z=\frac{d}{dt}(r\cos \theta )=\dot{r}\cos \theta +r(-\sin (\theta )\dot{\theta })$$ $$=\dot{r}\cos \theta -r\dot{\theta }\sin \theta$$

Recall steps to solve Lagrangian (5)

1. Find T
2. Find U
3. “Calculate” L = T-U
4. Euler-Lagrange equation

$$\frac{d}{dt}\frac{dL}{d{\dot{q}}_i}-\frac{dL}{d{q}_i}=0$$

5. Solve resulting diff eq.

Examples:

Harmonic Oscillator Setup: wall with spring, mass attached to spring position is defined as $x$ Equilibrium length of spring is $x_0$ with spring constant $k$

$$T=\frac{1}{2}m{\dot{x}}^2$$ $$U=\frac{1}{2}k(x-x_0{)}^2$$ $$L=T-U=\frac{1}{2}m{\dot{x}}^2-\frac{1}{2}k(x-x_0{)}^2$$ $$L=\frac{1}{2}(m{\dot{x}}^2-k(x^2-2x_{0}x+x_0^2))$$ $$L=\frac{1}{2}(m{\dot{x}}^2-k{x}^2-2x_{0}x+x_0^2)$$

Usually pick that $x_0$ is 0 and start measurements from that point. This is different

Do Euler-Lagrange

$$\frac{d}{dt}\frac{\partial L}{\partial \dot{x}}-\frac{\partial L}{dx}=0$$ $$\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$ $$\frac{d}{dt}(m\dot{x})=m\dot{x}$$ $$\frac{\partial L}{\partial x}=-k(x-x_0)$$ $$m\ddot{x}+k(x-x_0)=0$$ $$\ddot{x}=-\frac{k}{m}(x-x_0)$$

What we expect Solution:

$$A{e}^{i\omega t}+B{e}^{-i\omega t}$$

or sin/cos depending on your preference Harmonic Oscillator + Gravity Vertically hanging harmonic oscillator

$$T=\frac{1}{2}m{\dot{x}}^2$$ $$U=\frac{1}{2}k(x-x_0{)}^2+mgx$$ $$L=T-U=\frac{1}{2}m{\dot{x}}^2-\frac{1}{2}k(x-x_0{)}^2-mgx$$ $$\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$ $$\frac{d}{dt}\frac{\partial L}{\partial \dot{x}}=m\ddot{x}$$ $$\frac{\partial L}{\partial x}=-k(x-x_0)-mg$$ $$m\ddot{x}+k(x-x_0)+mg=0$$ $$m\ddot{x}=-k(x-x_0)-mg$$

Be careful how you define positive and negative

Newtonian and Lagrangian mechanics are $\equiv$ Consider newtons second law

$$\frac{m{d}^2\vec{x}}{d{t}^2}=\vec{F}(\vec{x},\vec{\dot{x}},t)$$

The general kinetic energy is given by

$$T=\frac{1}{2}m{v}^2$$

Now lets take the time derivative of the velocity derivative

$$\frac{d}{dt}\left(\frac{\partial T}{\partial \ddot{x}}\right)=m\ddot{x}$$

We now have the time derivative of the velocity derivative equal to force

$$\frac{d}{dt}\frac{\partial T}{\partial \ddot{x}}=F$$

Assuming conservative force

$$\vec{F}=-\vec{\nabla }u$$

So each component is equal to

$$F_{xi}=\frac{\partial u}{\partial x_i}$$

And now we rewrite newtons second law:

$$\frac{d}{dt}\frac{\partial T}{\partial \dot{x}}+\frac{\partial u}{\partial x}=0$$

Generalized:

$$\frac{d}{dt}\frac{\partial T}{\partial {\dot{x}}_i}+\frac{\partial u}{\partial x_i}=0$$

This leads us to the Euler-Lagrange equation. Cool We can say they are equivalent for the cases when the kinetic energy is independent of position. $\frac{dt}{d{x}_i}=0$ and when the potential energy is independent of velocity($\frac{du}{d{\dot{x}}_i}=0$) So $L=T-U$ gives us the same answer More explicitly:

$$\frac{d}{dt}\frac{\partial L}{\partial \dot{q_i}}-\frac{\partial L}{\partial q_i}$$

Example Pendulum

Pendulum with length $l$ , mass $m$ and displacement angle $\theta$ Use polar coordinates! Only one Equation of motion vs 2

$$T=\frac{1}{2}m({\dot{x}}^2+{\dot{y}}^2)$$ $$u=mgy$$ $$L=\frac{1}{2}m({\dot{x}}^2+{\dot{y}}^2)-mgy$$ $$x=l\sin \theta ;\dot{x}=l\dot{\theta }\cos \theta$$ $$y=-l\cos \theta ;\dot{y}=l\dot{\theta }\sin \theta$$ $$L=\frac{1}{2}m(l^2{\dot{\theta }}^2{\cos }^2\theta +l^2{\dot{\theta }}^2{\sin }^2\theta )+mgl\cos (\theta )$$ $${\sin }^2\theta +{\cos }^2\theta =1$$ $$L=\frac{1}{2}m{l}^2{\dot{\theta }}^2+mgl\cos \theta$$ $$\frac{dl}{d\dot{\theta }}=m{l}^2\theta ,\frac{d}{dt}\frac{dL}{d\dot{\theta }}=m{l}^2\ddot{\theta }$$ $$\frac{dl}{d\theta }=-mgl\sin \theta$$ $$\frac{d}{dt}\frac{dl}{d\dot{\theta }}-\frac{dl}{d\theta }=0$$ $$⟹m{l}^2\ddot{\theta }+mgl\sin \theta =0$$ $$\ddot{\theta }=-\frac{g}{l}\sin \theta$$

Solving using small angle approximation

Calculus of Variations

Based on Hamilton’s principle of least action Consider a dynamical system that moves from point 1 to point 2 within a specified time interval, $dt$. System goes from 1 $\to$ 2 in time $dt$

In all of the paths along which that dynamical system will move along, the actual path which is followed is the one that minimizes the action.

What the hell does that mean? “The action” The combination of kinetic and potential energies, aka the Lagrangian

Hacky sack! Point 1 is Prof. martin’s hand. Point 2 is Nate’s hand. There are an infinite number of paths between these two points, but the minimum action path is taken by the object.

This is the time integral of the Lagrangian

$$d\underset{t_1}{\overset{t_2}{\int }}(T-U)dt=0$$

This is also used in quantum physics.

$$J=\underset{t_1}{\overset{t_2}{\int }}L(x,\dot{x},t)dt$$ $$dj=0$$

The mathematical foundation of Lagrange’s equation is the extremum principle

This is calculus of variations

Given a function $f(x)$, to find an extremum of $f(x)$ we look to see where the first derivative vanishes

$$\frac{df}{dx}=0$$

Now, we instead want to find the extremum of the integral

$$J=\underset{x_1}{\overset{x_2}{\int }}F(y(x),y^{\prime }(x),x)dx$$ $$y^{\prime }(x)=\frac{dy}{dx}$$

Rewrite y: $y(\alpha ,x)$

$$y(\alpha ,x)=y(0,x)+\alpha \eta (x)$$

When $\alpha =0$

$$y(\alpha =0,x)=y(0,x)$$

This is the function that minimizes J Constraints $\eta (x)$ has a continuous first derivative that vanishes at bounds $x_1,x_2$.

$$\frac{d\eta }{dx}\text{ exists}$$ $$\eta (x_1)=\eta (x_2)=0$$

So

$$y(\alpha ,x_1)=y(0,x_1)$$ $$y(\alpha ,x_2)=y(0,x_2)$$

With these requirements

$$J(\alpha )=\underset{x_1}{\overset{x_2}{\int }}F(y(\alpha ,x),y^{\prime }(\alpha ,x),x)dx$$ $$\frac{\partial J}{\partial \alpha }{|}_{\alpha =0}=0$$

Take derivatives

$$\frac{dJ}{d\alpha }=\frac{d}{d\alpha }\underset{x_1}{\overset{x_2}{\int }}F(y,y^{\prime },x)dx$$ $$=\underset{x_2}{\overset{x_2}{\int }}\left[\frac{\partial F}{\partial y}\frac{\partial y}{\partial \alpha }+\frac{\partial F}{\partial y^{\prime }}\frac{\partial y^{\prime }}{\partial \alpha }\right]dx$$ $$y=y(0,x)+\alpha \eta (x)$$ $$y^{\prime }(\alpha ,x)=\frac{dy}{dx}=\frac{dy(0,x)}{dx}+\alpha \frac{d\eta (x)}{dx}$$ $$\frac{dJ}{d\alpha }=\underset{x_1}{\overset{x_2}{\int }}\left[\frac{dF}{dy}\eta (x)+\frac{dF}{d{y}^{\prime }}\frac{d\eta (x)}{dx}\right]dx$$

Now lets use integration by parts for the second term

$$\underset{x_1}{\overset{x_2}{\int }}\frac{dF}{d{y}^{\prime }}\frac{d\eta (x)}{dx}dx$$ $$u=\frac{dF}{d{y}^{\prime }}$$ $$du=\frac{d}{dx}\frac{dF}{d{y}^{\prime }}$$ $$dv=\frac{d\eta }{dx}$$ $$v=\eta$$ $$\int udv=uv-\int vdu$$ $$\underset{x_1}{\overset{x_2}{\int }}\frac{df}{d{y}^{\prime }}\frac{d\eta }{dx}dx=\frac{dF}{d{y}^{\prime }}\eta {|}_{x_1}^{x_2}-\underset{x_1}{\overset{x_2}{\int }}\frac{d}{dx}\frac{dF}{d{y}^{\prime }}\eta (x)dx$$

$\eta (x)=0\therefore$ middle term is 0

$$\frac{dJ}{d\alpha }=\underset{x_1}{\overset{x_2}{\int }}\left[\frac{dF}{dy}\eta (x)-\frac{d}{dx}\frac{dF}{d{y}^{\prime }}\eta (x)\right]dx$$ $$=\underset{x_1}{\overset{x_2}{\int }}\left[\frac{dF}{dy}-\frac{d}{dx}\frac{dF}{d{y}^{\prime }}\right]\eta (x)dx=0$$

Euler Lagrange equation comes from calculus of variations For non-trivial equations (aka ${\eta }_{9}x\ne 0$) we find

$$\frac{dF}{dy}-\frac{d}{dx}\frac{dF}{dy}=0$$

Euler Lagrange equation!