Continued from 2024-02-02 General Coordinates Continued
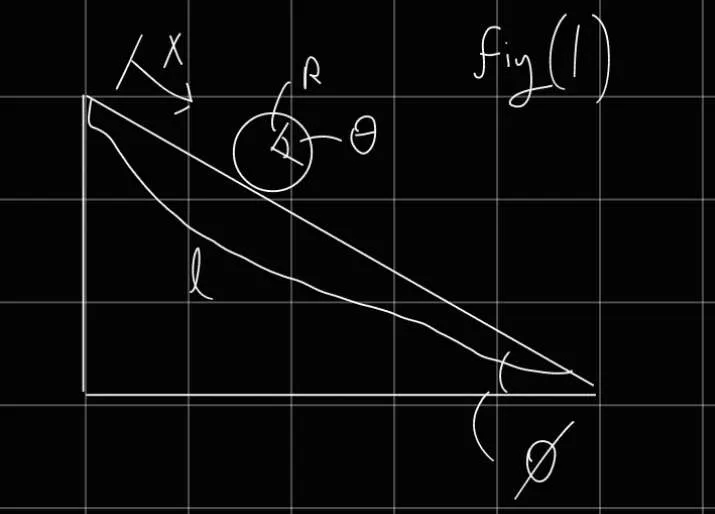
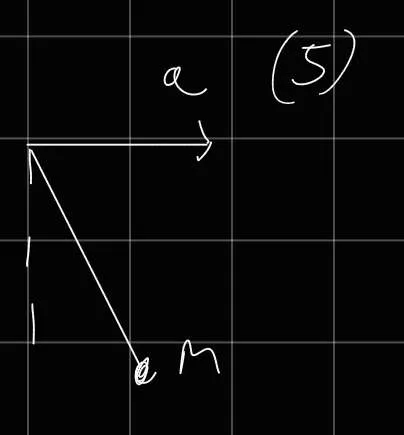
We went briefly over two methods to solve the ball rolling down a slope problem. Here is the first method, Substitution
L = 2 1 M x ˙ 2 + 2 1 I R 2 x ˙ 2 − M g ( l − x ) sin ϕ d t d ∂ x ˙ ∂ L − ∂ x ∂ L = 0 ∂ x ˙ ∂ L = M x ˙ + R 2 I x ˙ ( 1 ) d t d ( Equation 1 ) = M x ¨ + R 2 I x ¨ ∂ x ∂ L = M g sin ϕ ( M + R 2 I ) x ¨ − M g sin ϕ = 0 x ¨ = M + R 2 I M g sin ϕ Method 2, using Lagrange Multipliers
L ~ = L + λ f = 2 1 x ˙ 2 M + 2 1 I θ ˙ 2 − M g ( l − x ) sin ϕ + λ ( x − Rθ ) Resulting equations:
For x
d t d ∂ x ˙ ∂ L ~ − ∂ x ∂ L ~ = 0 ∂ x ˙ ∂ L ~ = M x ˙ d t d ∂ x ˙ ∂ L ~ = M x ¨ ∂ x ∂ L ~ = M g sin ϕ + λ M x ¨ − M g sin ϕ − λ = 0 ( 2 ) For θ
d t d ∂ θ ˙ ∂ L ~ − ∂ θ ∂ L ~ = 0 d t d ∂ θ ˙ ∂ L ~ = I θ ¨ ∂ θ ∂ L ~ = − R λ I θ ¨ + λ R = 0 Use Acceleration relationships
θ ¨ = R x ¨ I R x ¨ + λ R = 0 → λ = − R 2 I x ¨ Plug into equation 2
M x ¨ − M g sin ϕ + R 2 I x ¨ = 0 x ¨ ( M + R 2 I ) = M g sin ϕ x ¨ = M r + R 2 I M g sin ϕ This matches the last equation! they both give the right answer. Lets solve for λ
λ = ( M + R 2 I ) R 2 − M g sin ϕ I = M R 2 + I − M g sin ϕ I What is λ forces of constraint (singular). It turns out that in this equation, it is the force of friction on the ball.
For a disk I = 2 1 M R 2
x ¨ = M + 2 1 M M g sin ϕ = 3 2 g sin ϕ λ = M R 2 + 2 1 M R 2 − M g sin ϕ ( 2 1 M R 2 ) = − 3 1 M g sin ϕ
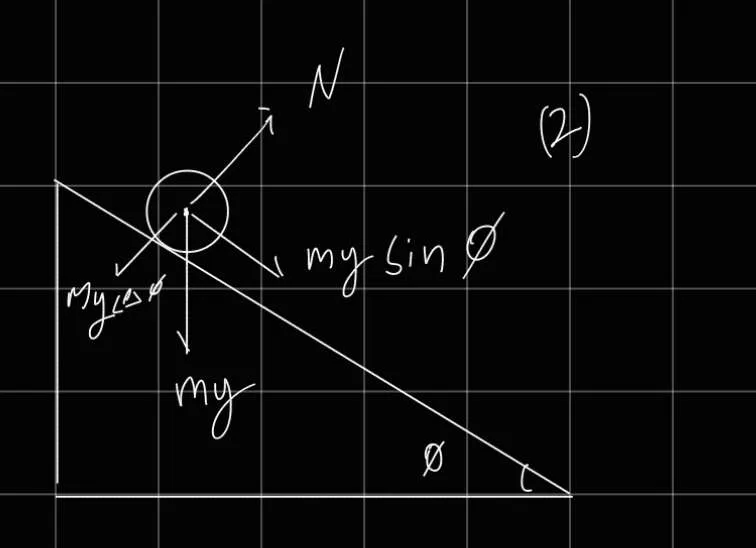
∑ F = m x ¨ m g sin ϕ − F = M x ¨ m g sin θ − R 2 I x ¨ = m x ¨
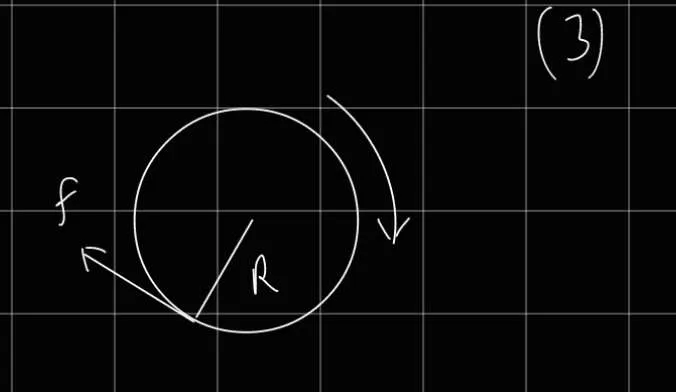
T = I α = r × F ⟹ I α = R f R I x ¨ = R f f = R 2 I x ¨
NB: there will be problems on the exam that require classical Newtonian mechanics
Conservation laws in Lagrangian Motion
Conservation of energy
If the following is true, energy is conserved
1:
∂ t ∂ L = 0 Time is homogeneous, L is invariant under translation in time.
No explicit time-dependent forces of constraint
2: Kinetic energy is only a function of generalized velocity
T ( q ˙ j ) ∝ q ˙ j q ˙ k 3: Velocity and time are independent
u = u ( q j ) Generalized Lagrangian is
L = L ( q j , q ˙ j ) = T ( q ˙ j ) − u ( q j ) d t d L ( q j , q ˙ j , t ) = j ∑ [ ∂ q j ∂ L q ˙ j + ∂ q ˙ j ∂ L q ¨ j ] + ∂ t ∂ L = 0 Remember:
d t d ∂ q ˙ ∂ L − ∂ q ∂ L = 0 → ∂ q ∂ L = d t d ∂ q ˙ ∂ L d t d L = j ∑ [ d t d ∂ q ˙ j ∂ L q ˙ j + ∂ q ˙ j ∂ L q ¨ j ] d t d l = j ∑ ⋯ = 0 so the sum has to be a constant
d t d [ L − j ∑ q ˙ j d q ˙ j d L ] = 0 we can call this constant − H
− H = L − j ∑ q ˙ j ∂ q ˙ j ∂ L for H is constant if ∂ t ∂ L = 0
H = j ∑ q ˙ j ∂ q ˙ j − L ∂ L = E Show H = E
Remember T ( q ˙ j ) ∝ q ˙ j q ˙ k
∂ q ˙ j ∂ L = ∂ q ˙ j ∂ ( T − u ) = ∂ q ˙ j ∂ T if u = u ( q j )
H = ∑ q ˙ j ∂ q ˙ j ∂ T − L = j ∑ q ˙ j ∂ q ˙ j ∂ T − ( T − u ) T = j 1 k ∑ a j , k q ˙ j q ˙ k ∂ q ˙ l ∂ T = k ∑ q l , k q ˙ k + j ∑ a j l q ˙ j l ∑ q ˙ l ∂ q ˙ l ∂ L = l , k ∑ a l , k q ˙ l q ˙ k + l , j ∑ a j , l q ˙ j q ˙ l = 2 T So
H = j ∑ q ˙ j ∂ q ˙ j ∂ L − L = 2 T − ( T − u ) = 2 T − T + u = T + u = E total This is the Hamiltonian , the same one from Quantum Physics
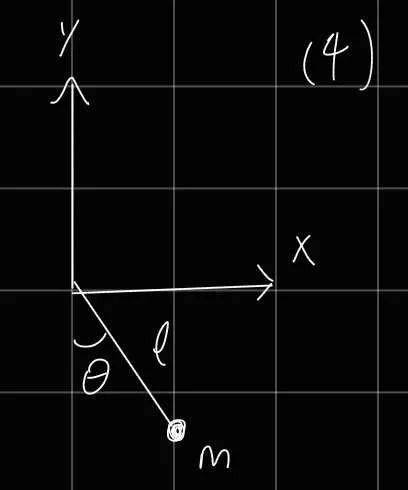
L = T − u = 2 1 m ( x ˙ 2 + y ˙ 2 ) − m g y x = l sin θ ⟹ x ˙ = l θ ˙ cos θ y = − l cos θ ⟹ y ˙ = l θ ˙ sin θ H = j ∑ q ˙ j ∂ q ˙ j ∂ L ⟹ H = θ ˙ ∂ θ ˙ ∂ L − L However, lets look at an accelerated pendulum -
L = T − u = 2 1 m ( x ˙ 2 + y ˙ 2 ) − m g y x = l sin θ + 2 1 a t 2 x ˙ = a t + l θ ˙ cos θ y = − l cos θ y ˙ = l θ ˙ sin θ x 2 = a 2 t 2 + l 2 θ ˙ 2 cos 2 ( θ ) + 2 a tl θ ˙ cos θ where ∂ t ∂ L = 0
L = 2 1 m [ a 2 t 2 + l 2 θ ˙ 2 + 2 a tl θ ˙ 2 cos θ ] + m g l cos θ its not conserved. Makes sense because the system is accelerating
Conservation of momentum
1: Space is homogeneous, the Lagrangian is invariant under space translation in the direction of q j
∂ q j ∂ L = 0 ( 3 ) P j = ∂ q ˙ j ∂ L
This is our generalized momentum, conserved if (3) is true
In Cartesian coordinates:
∂ x ∂ L = 0 , P i = ∂ x ˙ i ∂ L is conserved Consider Euler-Lagrange Equation again
d t d ∂ q ˙ j ∂ L − ∂ q j ∂ L = 0 d t d ∂ q ˙ j ∂ L = ∂ q j ∂ L = 0 ? ∂ q j ∂ L = P ˙ j Force is the negative gradient of potential
If we look at the LHS of the above equation,
d t d ∂ q ˙ j ∂ L = 0 means that
∂ q ˙ j ∂ L = P j = constant Newton
d t d P = F Example: 3d projectile
F = 0 0 − m g L = 2 1 m ( x ˙ 2 + y ˙ 2 + z ˙ 2 ) − m g z ∂ x ∂ L = 0 → d t d ∂ x ˙ ∂ L = 0 ∂ x ˙ ∂ L = P x = constant ∂ y ∂ L = 0 ⟹ d t d ∂ y ˙ ∂ L = 0 ∂ y ˙ ∂ L = P y = constant ∂ z ∂ L = − m g P z = constant ∂ x ˙ ∂ L = m x ˙ ∂ y ˙ ∂ L = m y ˙ Another example: pendulum
Skipping setup, go straight to Lagrangian
L = 2 1 m l 2 θ ˙ 2 + m g l cos θ ∂ θ ∂ L = − m g l sin θ = 0 P θ = constant P 0 = ∂ θ ˙ ∂ L = m l 2 θ ˙ Angular Momentum