2024-03-22 Parallel Axis Theorem

Steiner’s Parallel Axis Theorem

It states

$$I_{ij}=J_{ij}-M(a^2{\delta }_{ij}-a_i{a}_j)$$

Where $I_{ij}$ is the center-of-mass inertia tensor and $J_{ij}$ is the inertia tensor a distance $a$ away from $I_{ij}$ . This does require that the axes of the two coordinate systems are parallel.

Example: Homogeneous Cube with origin at the corner of the cube.

$$\{\mathbf{I}\}=M{b}^2\left(\begin{array}{ccc}\frac{2}{3}& -\frac{1}{4}& -\frac{1}{4}\\ -\frac{1}{4}& \frac{2}{3}& -\frac{1}{4}\\ -\frac{1}{4}& -\frac{1}{4}& \frac{2}{3}\end{array}\right)=J_{ij}$$

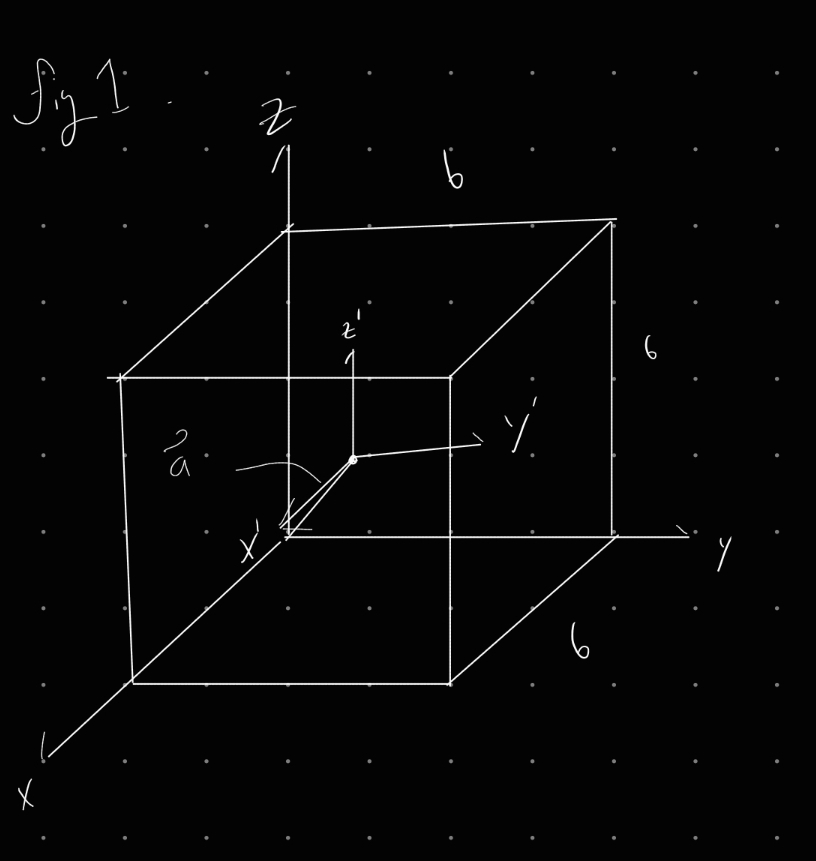Want origin at cube center $I_{ij}=?$

$$\vec{a}=\left(\frac{b}{2},\frac{b}{2},\frac{b}{2}\right)$$ $$a=\sqrt{{\left(\frac{b}{2}\right)}^2+{\left(\frac{b}{2}\right)}^2+{\left(\frac{b}{2}\right)}^2}=\sqrt{\frac{3b^2}{4}}$$ $$I_{ij}^{cc}=J_{ij}-M(a^2{\delta }_{ij}-a_i{a}_j)$$ $$I_{11}^{cc}=J_{11}-M(a^2-a_1{a}_1)$$ $$=\frac{2}{3}M{b}^2-M\left(\frac{3b^2}{4}-\frac{b^2}{4}\right)=\frac{1}{6}M{b}^2$$ $$I_{12}^{cc}=J_{22}-M(0-a_1{a}_2)$$ $$=\frac{1}{4}M{b}^2-M\left(-\frac{b^2}{4}\right)=0$$

Continue to find the rest

$$\{\mathbf{I}\}=\frac{1}{6}M{b}^2\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$$

Euler Angles

Transformation from one coordinate system to another through rotation

Represented as $\vec{x}=\lambda {\vec{x}}^{\prime }$ Where $\lambda$ is the rotation matrix comprised of 3 independent angles

Many choices but we use Euler’s angle $\varphi ,\theta ,\psi$ Start in x’ system and convert to x system in the following way

Remember the paul/emily/nate spinny coordinate thing

$${\lambda }_{\varphi }=\left(\begin{array}{ccc}\cos \varphi & \sin \varphi & 0\\ -\sin \varphi & \cos \varphi & 0\\ 0& 0& 1\end{array}\right)$$ $${\vec{x}}^{\prime \prime }={\lambda }_{\varphi }{\vec{x}}^{\prime }$$

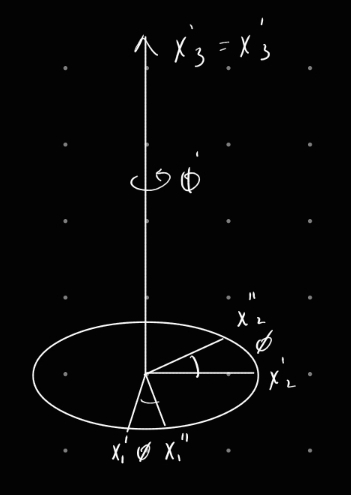
So we have rotation in the $x_1^{\prime }-x_2^{\prime }$ plane

Spun $\varphi$ around $x_3^{\prime }$ axis counterclockwise rotation

Next rotation counterclockwise around $x_1^{\prime \prime }$ axis through angle $\theta$

$${\lambda }_{\theta }=\left(\begin{array}{ccc}1& 0& 0\\ 0& \cos \theta & \sin \theta \\ 0& -\sin \theta & \cos \theta \end{array}\right)$$ $${\vec{x}}^{\prime \prime \prime }={\lambda }_{\theta }{\vec{x}}^{\prime \prime }$$

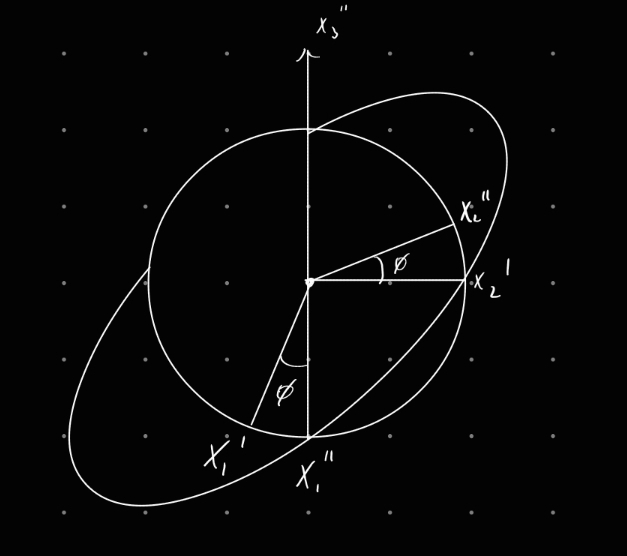
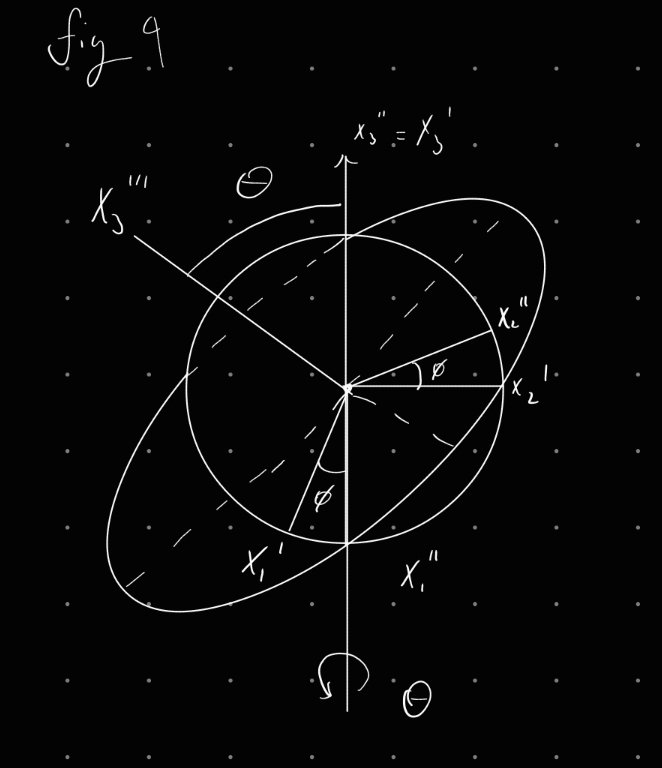
Finally rotate $\psi$ around $x_3^{\prime \prime \prime }$

fig 5

Combine to get

$$\vec{x}={\lambda }_{\psi }{\vec{x}}^{\prime \prime \prime }={\lambda }_{\psi }{\lambda }_{\theta }{\vec{x}}^{\prime \prime }={\lambda }_{\psi }{\lambda }_{\theta }{\lambda }_{\varphi }{\vec{x}}^{\prime }$$ $$\lambda ={\lambda }_{\psi }{\lambda }_{\theta }{\lambda }_{\varphi }$$

Rotation matrix is the following:

$$\begin{array}{c}{\lambda }_{11}=\cos \psi \cos \varphi -\cos \theta \sin \varphi \sin \psi \\ {\lambda }_{21}=-\sin \psi \cos \varphi -\cos \theta \sin \varphi \cos \psi \\ {\lambda }_{31}=\sin \theta \sin \varphi \\ {\lambda }_{12}=\cos \psi \sin \varphi +\cos \theta \cos \varphi \sin \psi \\ {\lambda }_{22}=-\sin \psi \sin \varphi +\cos \theta \cos \varphi \cos \psi \\ {\lambda }_{23}=-\sin \theta \cos \varphi \\ {\lambda }_{13}=\sin \psi \sin \theta \\ {\lambda }_{23}=\cos \psi \sin \theta \\ {\lambda }_{33}=\cos \theta \end{array}$$

At this point we could get into a discussion of rigid body Lagrangian problems using Euler rotation and Euler equations. We however will not do such things.