Rotational Kinetic Energy
Trot=21α∑mα(ω×rα)2(1)
Where
rα=(xα1,xα2,xα3…)ω=(ω1,ω2,ω3)
and
(A×B)2=A2B2−(A⋅B)2
Using these two relations we can rewrite (1) as the following
=21α∑mα[ω2rα2−(ω⋅rα2)]
Expanding this
Trot=21α∑mα[(i∑ωi2)(k∑xa,k2)−(i∑ωixα,i)(j∑ωjxα,j)]
Using Kronecker delta to simplify this:
21α∑i,j∑mα[ωiωjδij(k∑xαk2)−ωiωjxα,ixα,j]
=21ij∑ωiωjα∑mα[δijk∑xα,k2−xα,ixα,j]
Content after second summation is called the Inertia tensor
For a discrete distribution of particles, the inertia tensor looks like the following:
Iij=α∑mα(δijk∑xα,k2−xα,ixα,j)
Continuous Distribution
Iij=∫vp(r)(δijk∑xαk2−xαixαj)dV
Example:
Consider 3 masses (all with mass m) α will sum from 1→3 3D problem. They have the following positions:
x1=a,0,0x2=0,a,2ax3=0,2a,a
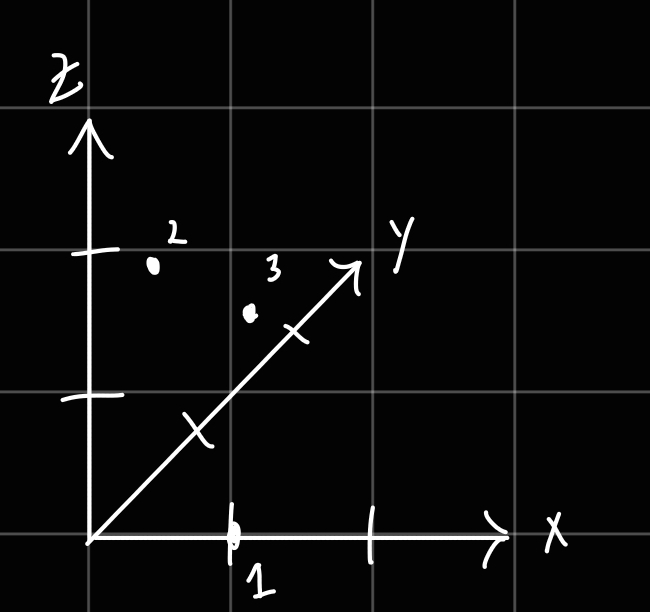
I11=α∑3mα(xα22+xα32)
=m[(x1,22+x1,32)+(x2,22+x2,32)+(x3,22+x3,32)]
=m[(02+02)+(a2+2a2)+((2a)2+a2)]
=m[a2+4a2+4a2+a2]=10ma2
Finding I22
α∑mα(xα,12+xα,32)
m[(x1,12+x1,32)+(x2,12+x2,32)+(x3,12+x3,32)]
m[a2+02+02+4a2+02+a2]
I22=6ma2
I33=m[a2+a2+4a2]=6ma2
I12=−m[(a×0)+(0×a)+(0×2a)]=0=I21
I13=−m[(a×0)+(0×2a)+(0×a)]=I3,1
I23=−m[(0×0)+(a×2a)+(2a×a)]=−4ma2=I32
{I}=10ma20006ma2−4ma20−4ma26ma2
Example:
Rectangular plate of uniform density ρ with total mass M, length a, width b and height c
- Put the origin at the center of the plate
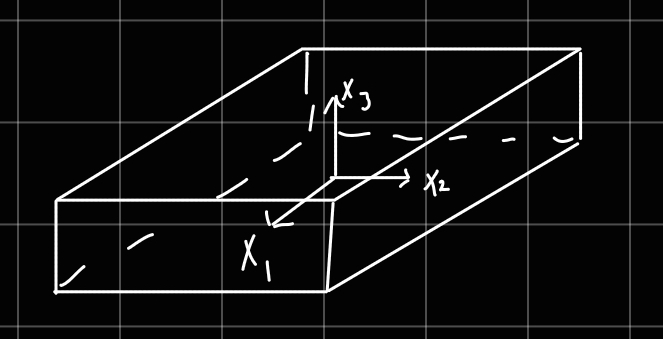
−2a≤x1≤2a−2b≤x2≤2b−2c≤x3≤2c
ρ=abcM
Iij=∫vρ(r)(δijk∑xαk2−xαixαj)dV
Iii=ρ∫V(x22+x32)dV=ρ[∫Vx22dV+∫Vx32dV]
ρ−2a∫a/2−2b∫b/2−2c∫c/2x22dx1dx2dx3+−2a∫a/2−2b∫b/2−2c∫c/2x32dx1dx2dx3
=ρ[ac31x23∣−b/2b/2+ab31x33∣−c/2c/2]
=ρ[ac318b3+ac8b331+ab8c331+ab8c331]
ρ[12ab3c+12abc3]=121abcM[ab3c+abc3]=121M[b2+c2]
I22=121M[a2+c2]
I33=121M(a2+b2)
I12=∫Vρ(−xα1xα2)dV−∫ρx1x2dV
=−ρ−c/2∫c/2dx3−b/2∫b/2x2dx2−a/2∫a/2x1dx1
=ρc(21x22∣−b/2b/2)(21x12∣−a/2a/2)
=−ρc[\cancelto0214b2−214b2]=[\cancelto0214a2−214a2]=0=I21
Similarly
I13=I31=0
I23=I32=0
{I}=121Mb2+c2000a2+c2000a2+b2
Trot=21ij∑2ωiωj
Particular case where ω=(0,0,ω3)
=21i=1∑3j=1∑3ωiωjIij
=21i=1∑3ωi[\cancelto0ω1Ii1+\cancelto0ω2Ii2+ω3Ii3]
=21I33ω32
The dzhanibhanibekov effect or tennis racket theorem arises from this ! very cool videos.

