2024-02-27 Collisions

Scattering Cross Sections

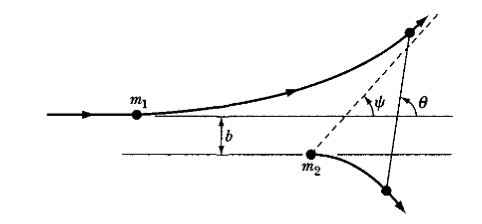In the above diagram, we have 2 particles, m1 and m2 with a repulsive force acting between them.

The impact parameter, $b$ represents the distance between m1 and m2 if there were no force. The impact parameter is related to the angular momentum, mass and potential energy in the following equation

l_{m_{1}} = m_{1} u_{1} b

This can be rewritten into the following with the equation for initial kinetic energy: $T_{0} = \frac{1}{2} m_{1} u_{1}^{2}$

l = b 2 m_{1} T_{0}

In some cases, we cannot take a measurement of $b$ . This is often the case in nuclear or atomic physics.
In these cases, we introduce the concept of a differential scattering cross section, denoted by $σ (θ)$
This is the measure of the number of interactions on the impacted particle that lead to scattering into the solid angle $d Ω^{'}$ at the angle $θ$ , over the number of particles incident per unit area. For example, if you have $d N$ particles scattered into $d Ω^{'}$ per unit time, then the probability is given by

σ (θ) d Ω^{'} = \frac{d N}{I}

Where I is the intensity of incoming particles

The relation between the impact parameter and scattering angle ( $Θ$ ) is given by the following equation

ΔΘ = r_{min} \int r_{max} \frac{l / r ^{2}}{2 μ [ E - U - ( \frac{l ^{2}}{2 μ r ^{2}} ) ]} d r

Central Force Problems

For rotational symmetry about the direction of motion of the incoming beam of particles we can define a ring around the approaching beam of thickness $d b$ like in the above figure. We can also set the angles $α$ and $β$ in the diagram below equal to each other, and $Θ$ , the scattering angle.

Therefore, $θ = π - 2Θ$ , and the scattering angle $Θ$ is given by the following integral

r_{min} \int \infty \frac{\frac{b}{r ^{2}}}{1 - ( \frac{b ^{2}}{r ^{2}} ) - ( \frac{U}{T _{0}^{'}} )} d r

using the modified initial kinetic energy equation from above, $l = b 2 μ T_{0}^{'}$

We can use this axial symmetry of the beam to Total potential energy

u = i = 1 \sum n u_{i} + i < j \sum u_{ij}

The first term is the potential from external forces, the second term is known as interaction potential.

2 particle collision

Recall there is Elastic collisions and Inelastic collisions

Consider a collisions in the lab frame:

\frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2} = \frac{1}{2} m_{1} v_{1}^{' 2} + \frac{1}{2} m_{2} v_{2}^{' 2}

Where $v_{i}^{'}$ is post collision velocity

Similarly:

m_{1} v_{1} + m_{2} v_{2} = m_{1} v_{1}^{'} + m_{2} v_{2}^{'} = m_{tot} V_{tot}

∴ \sum p_{i} = P_{tot}

Same collision viewed from thze center of mass frame

Since center of mass frame and center of mass at rest in the center of mass at rest in the center of mass frame are the same

v_{2}^{*} = \frac{m _{1}}{m _{2}} v_{1}^{*}, v_{2}^{*} = - \frac{m _{1}}{m _{2}} v_{1}^{' *}

Vectors are anti-parallel, means the two particles approach head on in the center of mass frame.

figure 1 here

Scattering angle is the same, not generally true in the lab frame.

Consider now kinetic energy in the center of mass frame:

\frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{*^{2}} = \frac{1}{2} m_{1} v_{1}^{*^{2}} + \frac{1}{2} m_{2} v_{2}^{' *^{2}}

This can be rewritten as

\frac{1}{2} m_{1} v_{1}^{*^{2}} + \frac{1}{2} m_{2} \frac{m _{1}^{2}}{m _{2}^{2}} v_{1}^{*^{2}} = \frac{1}{2} m_{1} v_{1}^{*^{2}} + \frac{1}{2} m_{2} \frac{m _{1}^{2}}{m _{2}^{2}} v_{1}^{' *^{2}}

\frac{1}{2}\left( m_{1}+\frac{m_{1}^{2}}{m_{2}} \right) \vec{v}_{1}^{*^{2}} = \frac{1}{2} \left( m_{1} + \frac{m_{1}^{2}}{m_{2}} \right)\vec{v}_{1}' ^{*^{2}}

Since elastic

T^{*} = T^{' *}

Meaning

∣ v_{1}^{*} ∣ = ∣ v_{1}^{' *} ∣

and

∣ v_{2}^{*} ∣ = ∣ v_{2}^{' *} ∣

Laboratory system:

insert figure 2 here

m2 is at rest

R = \frac{m _{1} r _{1} + m _{2} r _{2}}{m _{1} + m _{2}}

\dot{R} = \frac{m _{1}}{m _{1} + m _{2}} v_{1}

Center of mass system:

r_{1}^{*} = r_{1} - R

r_{2}^{*} = r_{2} - R

figure 3 here

Trajectories in lab frame

m_{1} v_{1} + m_{2} v_{2} = m_{1} v_{1}^{'} + m_{2} v_{2}^{'} = m \dot{R}

Seperating in 2d X component

m_{1} v_{1} = m_{1} v_{1}^{'} cos ψ + m_{2} v_{2}^{'} + cos ξ

Y component

0 = m_{1} v_{1}^{'} sin ψ + m_{2} v_{2}^{'} sin ξ

This is because the momentum upwards is the same as the momentum downwards

Trajectories in COM frame

figure 4

\dot{R} = 0 m_{1} v_{1}^{*} + m_{2} v_{2}^{*} = m_{1} v_{1}^{' *} + m_{2} v_{2}^{' *} = 0

Relationship between $ψ, ξ$ in lab frame with angle $θ$ in lab frame

r_{i}^{*} = r_{i} - R (1)

v_{i}^{*} = v_{i} - \dot{R} (2)

v_{i}^{' *} = v_{i}^{'} - \dot{R} (3)

R = \frac{m _{1} r _{1} + m _{2} r _{2}}{m _{1} + m _{2}}

\dot{R} = \frac{m _{1}}{m _{1} + m _{2}} \dot{v_{1}}

Break eq. 3 into components x:

v_{1}^{' *} cos θ = v_{1}^{'} cos ψ - \frac{m _{1}}{m _{1} + m _{2}} v_{1} (1a)

v_{1}^{' *} cos θ + \frac{m _{1}}{m _{1} - m _{2}} v_{1} = v_{1} cos ψ (2a)

v_{1}^{' *} sin θ = v_{1}^{'} sin ψ - 0 (3a)

$v_{1}$ is only in the x direction

v_{1}^{' *} sin θ = v_{1}^{'} sin ψ (4a)

\frac{( 4 a )}{( 2 a )} = \frac{v _{1}^{' *} sin θ}{v _{1}^{' *} cos θ \frac{m _{1}}{m _{1} + m _{2}} v _{1}} = tan ψ

v_{1}^{' *} = v_{1}^{*}

v_{1}^{' *} = v_{1} - \dot{R}

v_{1}^{*} = v_{1} - \frac{m _{1}}{m _{1} + m _{2}} v_{1} = v_{1} [\frac{m _{1} + m _{2}}{m _{1} + m _{2}} - \frac{m _{1}}{m _{1} + m _{2}}]

v_{1}^{*} = \frac{m _{2}}{m _{1} + m _{2}} v_{1} = v_{1}^{*^{'}}

tan ψ = \frac{sin θ}{cos θ + \frac{m _{1}}{m _{1} + m _{2}} v _{1} \frac{1}{v _{1}^{' *}}}

tan ψ = \frac{sin θ}{cos θ + \frac{m _{1}}{m _{2}}}

Testing this for edge cases

m_{1} ≪ m_{2} \to tan ψ \approx tan θ ∴ ψ \approx θ

m_{1} = m_{2} tan ψ = \frac{sin θ}{cos θ + 1} = tan \frac{θ}{2}

Similar correct method for product 2

tan ξ = tan (\frac{π}{2} - \frac{θ}{2})

m_{1} = m_{2} ξ + ψ = \frac{π}{2}

Paul's Physics Notes

Explorer

2024-02-27 Collisions

Scattering Cross Sections

Central Force Problems

2 particle collision

Trajectories in lab frame

Trajectories in COM frame

Graph View

Table of Contents

Backlinks